Contents
1.3 Partial Pressure 1.4 Fundamentals 1.5 Analysis of Mixtures 1.6 Boiling Point Calculation 1.7 Dew Point Calculation 1.8 Flash Calculation
1.1 INTRODUCTION
Like the molecules of gases, the molecules of a liquid are constantly in motion. Unlike the molecules of gases, the molecules of a liquid are held close together by natural attraction between the molecules. In a liquid, the attraction between molecules tends to keep each molecule confined to a small space. Within this space a molecule is usually in violent motion. The violent motion of the molecules at the surface of a liquid causes many of these molecules to escape from the liquid. If the temperature of a liquid is increased, the motion of the molecules becomes more violent.
When a liquid is placed in an open container and heated, both its vapor pressure and its rate of evaporation increase. When liquid in an open container is heated until the vapor pressure equals the pressure of the atmosphere, evaporation becomes very rapid, and the liquid boils.
1.4 FUNDAMENTALS
Fractional distillation is an operation which is based on the differences in volatility or different “escaping tendencies” of the products which have to be separated. It is obvious that for solving the numerous problems in technical fractionation a thorough knowledge of the fundamental laws and rules governing the volatility characteristics of systems consisting of two or more components is a prerequisite.
This law states that at a given temperature the partial vapour pressure of a relatively volatile substance above its solution (in a relatively non-volatile solvent) is proportional to its concentration in the solution.
1.4.2
The second important law underlying the theory of fractional distillation is Dalton Dalton
1.1 Introduction
1.2 Vapor Pressure
1.4.1 Henry’s Law
1.4.2 Dalton
Chapter 1
Theoretical Principles of Fractional Distillation
1.1 INTRODUCTION
A detailed discussion of the entire theory of fractional distillation and all the problems connected herewith is not possible within the scope of this Course and has not been attempted. The most important features of this vast subject have been dealt with and a number of references are given which should enable the reader to tackle any specific problem requiring a deeper knowledge of the various methods used in fractionation calculations. Since the majority of the Group's technologists are engaged in other fields than design work, complete discussion of tray-to-tray calculations has been omitted. However, it is felt that the technologist should be familiar with simple column evaluations, boiling point, dew point and flash calculations and be able to interpret intelligently design work should the necessity arise.
1.2 VAPOR PRESSURE
A gas or vapor consists of molecules in random and chaotic motion. Millions of small particles moving in all directions in the air in the room, they collide with each other repeatedly.
There are many collisions between molecules in a gas. The molecules of a vapor in a container repeatedly have collisions with the walls of the container. When many gas molecules collide repeatedly with the walls of a container, these collisions add up to a pressure exerted on the walls. If the temperature of a gas is increased, the molecules in the gas move faster. At a lower temperature, the vapor molecules move slower. The more rapid motion at higher temperatures results in more violent collisions of the molecules. As the molecules move faster and the collisions become more violent, molecules in a closed container strike the walls with more force. The pressure, therefore, increases.
The pressure of a gas in an open container cannot be increased, since some of the gas would escape to equalize the pressure with the surroundings. The pressure of a gas in an open container cannot be increased by increasing the temperature.
If an empty container is partially filled with liquid, molecules escape from the surface of the liquid, forming a vapor in the space above the surface. Gas molecules which strike the surface of a liquid tend to stick to the liquid. Thus, molecules may be escaping the liquid and returning to the liquid from the gas at the same time. When a vessel contains both a liquid and a vapor, molecules are continually going from the liquid to the vapor or gas and from the vapor to the liquid. When the number of molecules leaving the liquid equals the number entering the liquid, the gas and the liquid are said to be in equilibrium with each other. So at equilibrium, equal numbers of molecules pass between the liquid and the vapor, or gas.
When more molecules are escaping the liquid than returning, the liquid is said to be evaporating. The process in which a greater number of molecules leave the liquid than enters it is called evaporation. When more molecules are entering the liquid from the vapor than are escaping the liquid, the vapor is condensing. The process in which a greater number of molecules enter the liquid than leave it is called condensation.
When the temperature of a liquid is increased, the pressure of the vapor in equilibrium with it increases and maintains equilibrium. On the other hand, when the temperature of a liquid is decreased, the pressure of the vapor decreases and maintains equilibrium. When a liquid and a vapor are at equilibrium, the pressure of the vapor is called the vapor pressure of the liquid.
The pressure of a gas or vapor above the surface of a liquid in a closed container is not necessarily the same as the vapor pressure of the liquid. In order for the pressure of the gas to be equal to the vapor pressure of the liquid, the gas and the liquid must be in equilibrium with each other. When the temperature of a liquid in a closed container is increased, the pressure of the vapor increases until the vapor and the liquid are at equilibrium with each other.
If the pressure over a boiling liquid is increased, the boiling temperature is increased and if the pressure over a boiling liquid is decreased, the boiling temperature is decreased. Since the pressure of the atmosphere on the top of a mountain is lower than at sea level, liquids boil at lower temperatures on top of a mountain.
The vapor pressures for different liquids at the same temperature are not the same. Therefore, water and pentane have different vapor pressures at 100 °F. (Figure 1.1). The vapor pressure of pentane is 18 approximately pounds per square inch at 100°F. Water has a vapor pressure of 5 pounds per square inch at a temperature of 162 ºF. Recall that the vapor pressure of the liquid must be equal to the pressure of the surroundings for a liquid to boil. If the pressure of the atmosphere is 14.7 psi, water boils at 212°F. A pressure cooker cooks food faster than an open container, because the temperature inside is increased by the increase in pressure.
 |
Figure 1.1 Vapor Pressure of Water and Pentane |
1.3 PARTIAL PRESSURE
The pressure that a gas exerts on the walls of a container depends on the number of collisions between the molecules and the container wall. If more molecules are present, there are more collisions and a greater pressure. If two containers of the same volume are filled with gas to the same pressure and temperature, each contains the same number of gas molecules. For the same volume and temperature, the greater the number of molecules in a gas, the greater the pressure of the gas must be.
When two or more gases are mixed, each gas exerts a pressure on the walls of the container. Although these separate pressures cannot be measured, the total pressure can be measured. The total pressure of a gas mixture is equal to the sum of the pressures of the different gases in the mixture; the separate pressures of the gases are called partial pressures.
For a mixture of two gases, if the partial pressure of each gas is the same, there must be equal numbers of each kind of molecule. If a tank contains 5 times as many ethane molecules as propane molecules, the partial pressure of ethane is 5 times as great as propane, the gas is said to be richer in ethane. When two or more pure liquids (or gases) are mixed, the components of the mixture are the original pure liquids, or substances. Enrichment is a process by which a mixture (for example, a mixture of several gases) becomes more pure, enriched, or rich in one of its components.
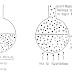
If a closed container is partially filled with a mixture of two liquids, molecules of both liquids escape to the gas from the liquid and return to the liquid from the gas. When the number of molecules escaping equals the number returning- for both components, the gas and the liquid are said to be at equilibrium with each other. At equilibrium, the number of molecules escaping from the liquid is equal to the number returning to the liquid for each component. The drawing shows a tank containing a mixture of two components, one heavy and one light. An example of such a system would be butane-hexane, where butane would be the light molecules and hexane the heavy molecules.
At equilibrium the number of light molecules escaping from the liquid is equal to the number returning to the liquid. Also, at equilibrium the number of heavy molecules escaping from the liquid is equal to the number of heavy molecules returning to the liquid. However, at equilibrium the number of light molecules escaping and returning to the liquid is not equal to the number of heavy molecules escaping and returning to the liquid. Light molecules are able to escape the liquid more rapidly than the heavy ones. Therefore, at equilibrium, there are more light molecules escaping and returning to the liquid. Because the light molecules are able to escape the liquid faster than the heavy ones, the light molecules tend to concentrate or to be enriched in the vapor. For example, if the liquid contains half light and half heavy molecules at equilibrium, the gas contains more light molecules than heavy molecules.
When the gas and the liquid are at equilibrium, the gas is richer in the light component and the liquid is richer in the heavy component. Therefore, if a liquid mixture is partially vaporized, the light component in the vapor becomes more concentrated than the light component in the liquid. In other words, the vapors are enriched in the lighter component.
1.4 FUNDAMENTALS
1.4.1 Henry's Law
This can be expressed by:
Pi = Ci xi …………………………………………….. (1)
Where xi = mole fraction of a certain component in the liquid,
Pi = partial vapour pressure of this component,
Ci = proportionality factor.
In general, this law holds only for low concentrations of component “i”. In certain cases, however, it is applicable throughout the entire range of concentrations. Such solutions are said to behave ideally and on extrapolating Henry's law in such cases to the pure compound (i.e. increasing the concentration of the dissolved substance) we see that, since when xi becomes 1, Ci equals Pi, this factor is then equal to the vapour pressure (Pi) of the pure substance and to the system pressure.
Thus the mathematical expression becomes:
Pi = Pi xi …………………………………………….. (2)
In this form and restricted to ideal solutions Henry's law is known as Raoult's law.
Many hydrocarbon systems closely approach the hypothetical ideal solution and Raoult's law can therefore be applied in these cases without introducing too serious an error. Mixtures of paraffin and naphthene are, in general, very nearly ideal, while mixtures of aromatics with naphthenes or paraffins are further away from ideal solutions.
It must be realized, however, that ideal behaviour only occurs with substances as closely related as hydrocarbons, and is most uncommon for other instances.
A particularly simple case where Raoult's law is not valid is the case of two or more components completely immiscible in the liquid phase. In this case the total pressure is independent of the relative amounts in which these components are present and is simply equal to the sum p =sum Pi of the vapour pressures of the pure components at the given temperature. The total pressure is therefore higher than the vapour pressure of any component. Such a system is called a pseudo-azeotrope.
1.4.2 Dalton
Pi = P Yi and
sum. Pi =P …………………………. (3)
Where Pi= partial pressure of component “i”,
P = total pressure of system,
Yi = mole fraction of component “i” in the vapour phase.
It follows from (2) and (3) that
Pi xi = P Yi
From equation (4) (known as Raoult-Dalton's law) it follows that the concentration of any component in a vapour which is in equilibrium with a liquid mixture can be calculated by multiplying the concentration of that component in the liquid phase by the ratio of the vapour pressure of the pure component to the total pressure of the system. All concentrations are to be expressed as mole fractions.











Post a Comment